সব Trapezium কিন্তু Parallelogram নয়

প্রথমে এসেছিলো ট্রাপিজিয়াম। একা নয়। তিন জন।

ব্যাপারটা খোলসা করা যাক। প্রথমে একটা ত্রিভুজ এঁকে ফেলো গ্রাফ পেপারে। প্রতিটা বিন্দুর একটা করে coordinate থাকবে।

ত্রিভুজটার ক্ষেত্রফলের একটা ফর্মুলা খোঁজা যাক। এমনিতে ত্রিভুজের ক্ষেত্রফল হচ্ছে

$$ \frac{1}{2} \times base \times height $$

কিন্তু আমরা ঠিক তেমন ফর্মুলা চাইছি না। আমরা কোনবিন্দুদের coordinate দিয়ে ক্ষেত্রফল লিখে ফেলতে চাই।

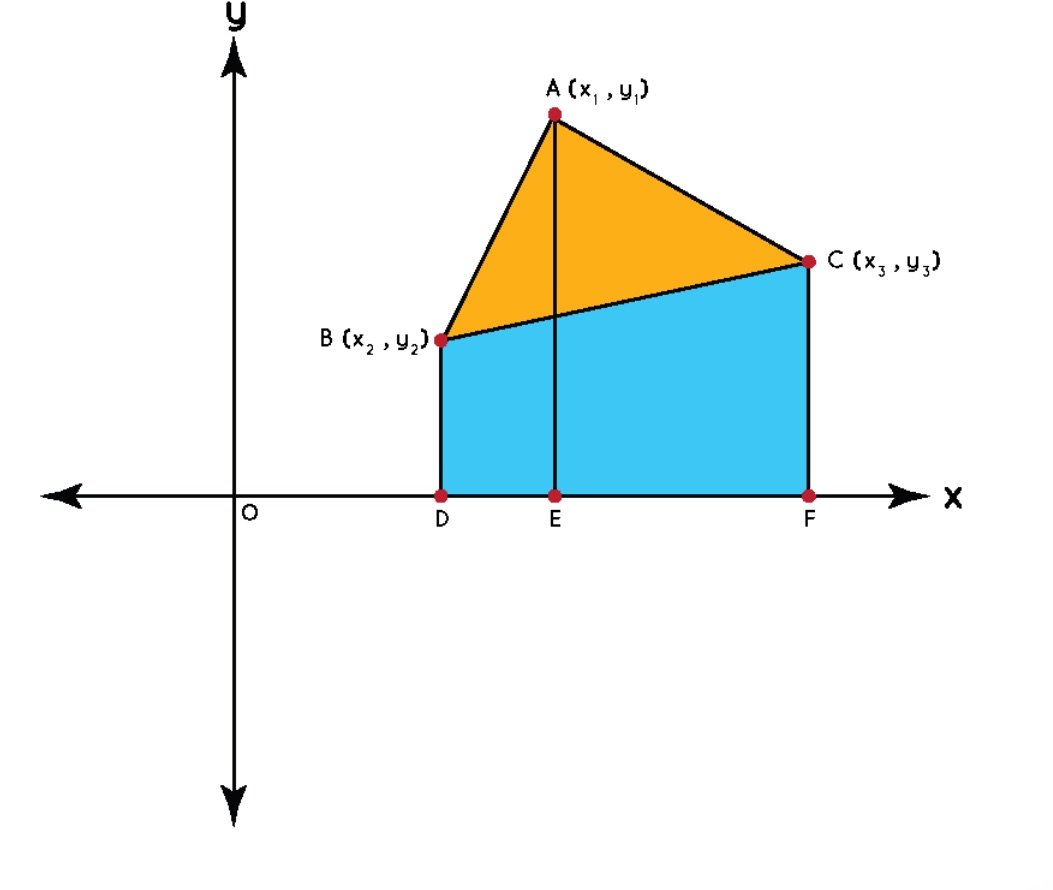
তিনটে কোন থেকে x-axis-এর ওপক লম্ব (perpendicular) এঁকে নাও। সহসা তিনটে ট্রাপিজিয়াম আবির্ভুত হবে।

দুটো ট্রাপিজিয়াম যোগ করে একটা বিয়োগ করলে, ত্রিভুজের ক্ষেত্রফল পাওয়া যাবে।

$$ ABDE + ACFE – BCFD = \Delta ABC $$

Trapezium -এর ক্ষেত্রফলের সূত্র বেশ সোজা। সমান্তরাল দুটো বাহু যোগ করো। যোগফল-কে সমান্তরাল বাহুর দুরত্ত্ব দিয়ে গুণ করো। শেষমেশ ২ দিয়ে ভাগ করে দাও। ব্যাস হয়ে গেলো।

$$ \frac{1}{2} \times \textrm{(sum of parallel sides)} $$

$$ \times \textrm{(distance between parallel sides)} $$

(এই সূত্রটা ওই ত্রিভুজের ক্ষেত্রফলের সূত্র থেকেই পাওয়া যায়। Trapezium-কে দুই টুকরো করে নাও যে কোনো diagonal এঁকে। তারপর সেই ত্রিভুজ টুকরো দুটোর ক্ষেত্রফল যোগ করো।)

অতএব লিখে ফেলা যাক পুরোটাঃ

$$ ABDE + ACFE – BCFD = \Delta ABC $$

$$ ABDE = \frac{1}{2} \times (y_1 + y_2) \times (x_1 – x_2) $$

$$ ACFE = \frac{1}{2} \times (y_1 + y_3) \times (x_3 – x_1) $$

$$ BCFD = \frac{1}{2} \times (y_2 + y_3) \times (x_3 – x_2) $$

ব্যস আর কি! দুটোকে যোগ করে একটাকে বিয়োগ করে দাও।

Coordinate দিয়ে ত্রিভুজের ক্ষেত্রফল লিখতে গেলে, তোমায় Trapezium-কে ছুঁয়ে আসতে হবে। এবার প্রশ্ন হলো এই তিনটে ট্রাপিজিয়াম কখন parallelogram হতে পারে? মনে মনে ভাবো যে BC হচ্ছে x-axis-এর সমান্তরাল। তা হলে BCFD হয়ে যাবে paralleogram। বাকি দুটো Trapezium কিন্তু parallogram হবে না। এক কাজ করো। A বিন্দুকে ক্রমশ BC-র দিকে নামিয়ে আনো। দেখবে ABDE আর ACFE ক্রমশ parallelogram হয়ে উঠছে। যেই না A বিন্দুটা BC স্পর্শ করবে, তারা parallelogram হয়ে যাবে। ত্রিভুজের ক্ষেত্রফল হয়ে যাবে ০।

তাহলে এভাবে ভাবতে পারো যে trapezium দুটোর parallelogram না হওয়ার কারণ হলো A বিন্দুর মাথা উঁচিয়ে থাকা। সে মাথা নামালেই সব সমান্তরাল হয়ে যাবে।